One of the benefits of graphing calculators and graphing software is that it allows you to learn things about functions and equations that would have been tedious to explore via pencil and graph paper. Families of graphs is a concept that starts with a “parent” function or equation and asks you to compare “child” functions or equations to it to determine how they have translated or transformed from the original.
Consider, for example one of the easiest equations to graph:
y = x or f(x) = x in functional notation.
When you plug values into the independent variable, x, the dependent variable, y, has the same value. When x is 1, y is 1. When x is 2, y is 2. When x is -4, y is -4. Plotting the points on a coordinate plane result in a line that goes through the origin, rising to the right as much as it runs.
So if y = x is the parent equation, compare the following to it.
y = x +5
y = x – 2
y = x + 3
y = x – 1
Next graph y = |x|, the parent and compare it to the following children:
y = |x| + 1
y = |x| + 2
y = |x| – 3
y = |x| – 4
What do you notice?
Compare y = |x| to the following:
y = |x – 2|
y = |x – 1|
y = |x + 4|
y = |x + 2|
Did they behave as you expected?
Compare the graph of the parent y = x² with the graphs of the following equations. How are they changed from the original?
y = x² – 3
y = x² + 1
y = (x – 4)²
y = (x + 2)²
y = (x + 2)² + 3
Returning to our original line y = x, what happens when we multiply x by a number?
y = ½ x
y = 3x
y = -¾ x
y = -2 x
Do your explanations hold for the following?
y = |x| and y = -|x|
y = x² and y = ¼ x²
y = x² and y = -3x²
y = x³ and y = -x³
Use the Families of Graphs Exploration to sketch the graphs and note your observations.
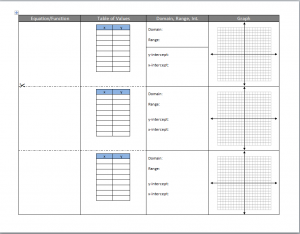
A Parent Functions Foldable is available for note taking.
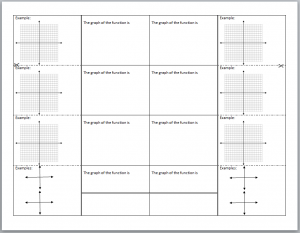
A Functions Transformations Foldable is available for note taking. Inspiration by Sarah Hagan.










Dear Stacie,
I am loving your webiste. The practical and visual way you communicate is outstanding.
I am working with a group of educators and would like permission to share an example of your note taking foldables.
Please contact me at the email provided if it would be ok to share the image of the function transformation foldable.
Kind regards
Lyn
Thank you! I wish I had more time to be creative this year but I’m barely staying afloat. Please share any of the foldables with anyone who can use them in their classes.