My regular geometry students have struggled with the concept of which side measures can form a triangle. I don’t know if it’s the wording of theorem – the sum of any two sides of a triangle must be greater than the third – there are a lot of math words there, or if it’s that they are being told the information instead of discovering the concept themselves.
Last year I bought a package of white pipe cleaners and marked off 1 inch markings with a Sharpie. I distributed one to each student and asked them to try to form triangles with the side lengths I listed. In hind sight, I should have put them in pairs or small groups with a handout. It didn’t bridge the gap and I had a lot of rolled up pipe cleaners and had to count them all to ensure I would get them back for the next class’ use. Apparently pipe cleaners are a lot of fun for teens or they are so starved for play that anything will do.
I’ve mulled over it for a while and came up with two options to try.

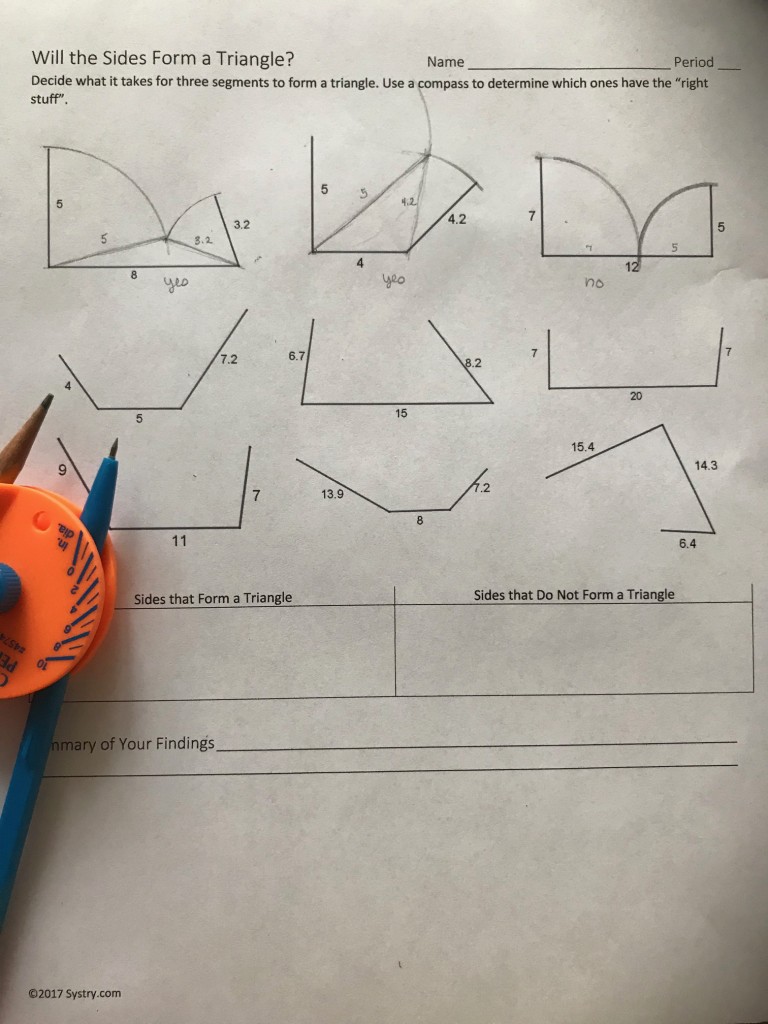
The first would require students place the compass point on the “hinges” of the potential triangle and swing an arc that is the length of each of the other two segments to see if they meet.
In the second, I created strips that are between 1 and 18 centimeters in length with the intent that they cut them out and decide if they will form a triangle. Knowing that class time is precious and fearing the time wasted in cutting out strips of paper, I broke out some bamboo skewers and cut them to size. I thought they could use the handout as a template so they could find the necessary sizes for each triple. Cutting the bamboo skewers was doable with a wire cutters, but time consuming.
Then I thought about spaghetti. What if I give my students some pieces of uncooked spaghetti and ask them to break them into the necessary lengths?
Thoughts? What has worked well for you?
Update:
I found plastic stir sticks that work really well. They are durable and much easier to cut. The template helped them determine size without needing to measure. They made a lot of difference in understanding whether three sides will form a triangle. The updated simplified handout on page 2 is also here: Will the Sides Form a Triangle Investigation.





Leave A Comment