The midpoint formula and the distance formula are introduced in algebra class. If students do not get a chance to discover how they are derived, they become yet another set of equations and processes to memorize.
The activity below gives students an opportunity to discover the formulas or re-discover them. The Pythagorean Theorem is sprinkled in so students may need some refreshing on how and why it works.
The two real world applications below are in the explorations pdf. The first is an application of the Pythagorean Theorem. The second requires the use of the Midpoint Formula.
Calculating Distances
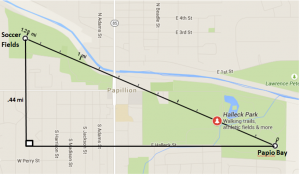
After swimming at the Papio Bay Aquatic Center, you walk 1.28 miles via the park to the soccer fields. How much further would you have walked if you had followed the city streets moving in west and north directions?
Applying the Midpoint Formula
Three identical frames will be purchased for a photo collage. If the name for one frame will be placed 72” from the corner and 43” up from the landing and the nail for another frame will be placed 92” from the corner and 29” up, where should the nail for the third frame go if it is to be hung midway between the other two?







Leave A Comment