There are three types of graphical symmetry you may be responsible for: x-axis, y-axis, and origin. Knowing the properties of symmetry can help you when sketching complex graphs.
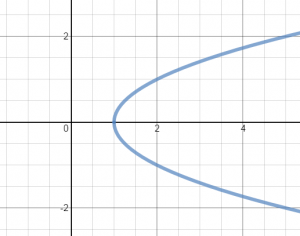
x-Axis Symmetry
If an equation or function is symmetric with respect to the x-axis. you can fold the paper it is graphed on along the x-Axis and the halves of the graph will line up. If the ordered pair (x, y) is a solution to the equation and the equation is symmetric to the x-axis, then (x, -y) will also be a solution.
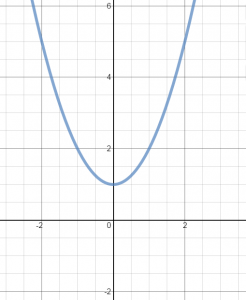
y-Axis Symmetry
An equation or function that is symmetric with respect to the y-axis has (x, y) and (-x, y) as solutions. Likewise, if you switch -x for x in the original equation, the result should be the original equation when simplified.
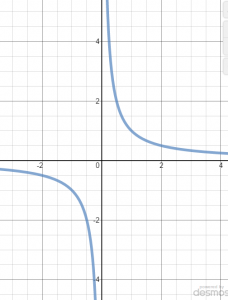
Origin Symmetry
Equations or functions that are symmetric to the origin have ordered pairs (x, y) and (-x, y). If you switch -x for x and -y for y in the original equation and simplify, if you get the original equation, it is symmetric with respect to the origin.
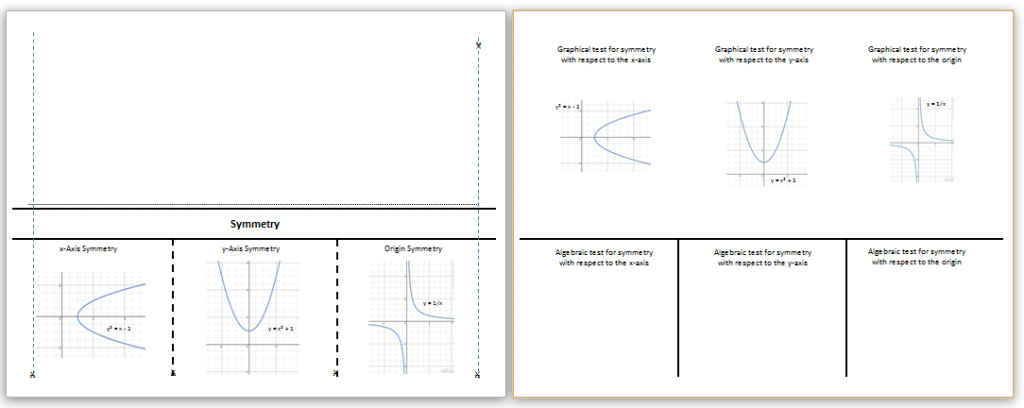
The Graphical Symmetry Foldable can be added to an interactive notebook to help students remember key concepts. Be sure to rotate it when printing or copying.



Leave A Comment