I was thinking about a way to make square roots more visual for my students. With graph paper, I started sketching out the perfect squares and then played with numbers that form rectangles rather than squares. The video below shows the process.
Ideally, students would be introduced to this method in middle school and then be ready for more abstraction of the concept in algebra I. I have roughly an even split each year of regular geometry students who can and can not simplify square roots with ease. Which complicates things when we get to the special right triangles unit.
In my mind the progression would be to introduce this in 7th or 8th grade math. Demonstrate the process and hand out grid paper. Then let students in groups of 2 – 4 choose from a list of non-perfect squares to simplify. When they are successful with one number, hang it on the board and give the group (or let them choose) another. Then as a whole class activity discuss what they notice, what they wonder, and see if there’s a pattern to which numbers can be simplified and which can not.
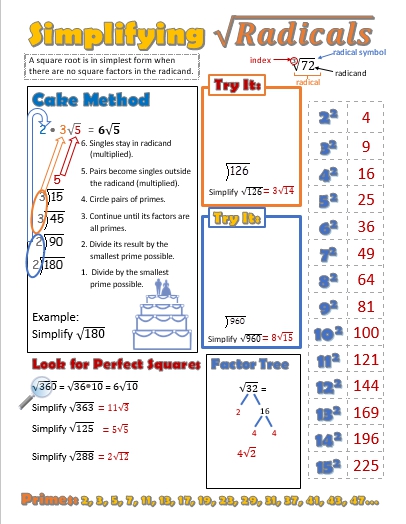
Then in algebra I ask students to simplify radicals by using factor trees, identifying perfect squares, or the “cake” method. Some remediation would be needed, of course in geometry, but special right triangles and the introduction to trig wouldn’t be such a mountain to climb with simplifying radicals mastered.


Please can you write an article instead of one video to explain it all