I remember being frustrated last year at about this time with my geometry students’ performance on four questions on their circles test. The test was chronologically ordered in the way the material was presented so I was perplexed when they did poorly on the last section before review. It involved circles in the coordinate plane. Below are the questions from one of the forms of the test.
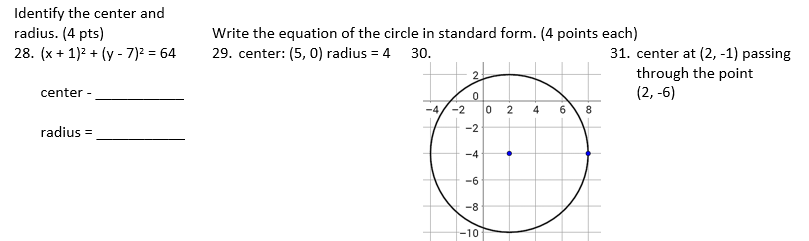
On the day I presented the lesson, I gave them a rudimentary form of Vizual Notes and I remember several students in my various sections comment “this is easy. To find the center, just change the signs of the points.” I anticipated some might struggle with the last question because it involves using the distance formula if you don’t notice the x-coordinates are the same. I teach non-honors geometry.
In my heart, I know that telling students “Here’s the standard form of the equation of a circle and here are the center and the radius.” is not the best way to teach, nor the best way to learn. So, before I finished grading the tests, I wrote this Desmos activity. I was careful to add a note to self in my Google Calendar so I wouldn’t forget to use it with students the following year.
This week, when I checked for laptop/iPad cart availability, it was a no-go. All were checked out during the periods I needed them. So plan B was to create a pencil/paper investigation.
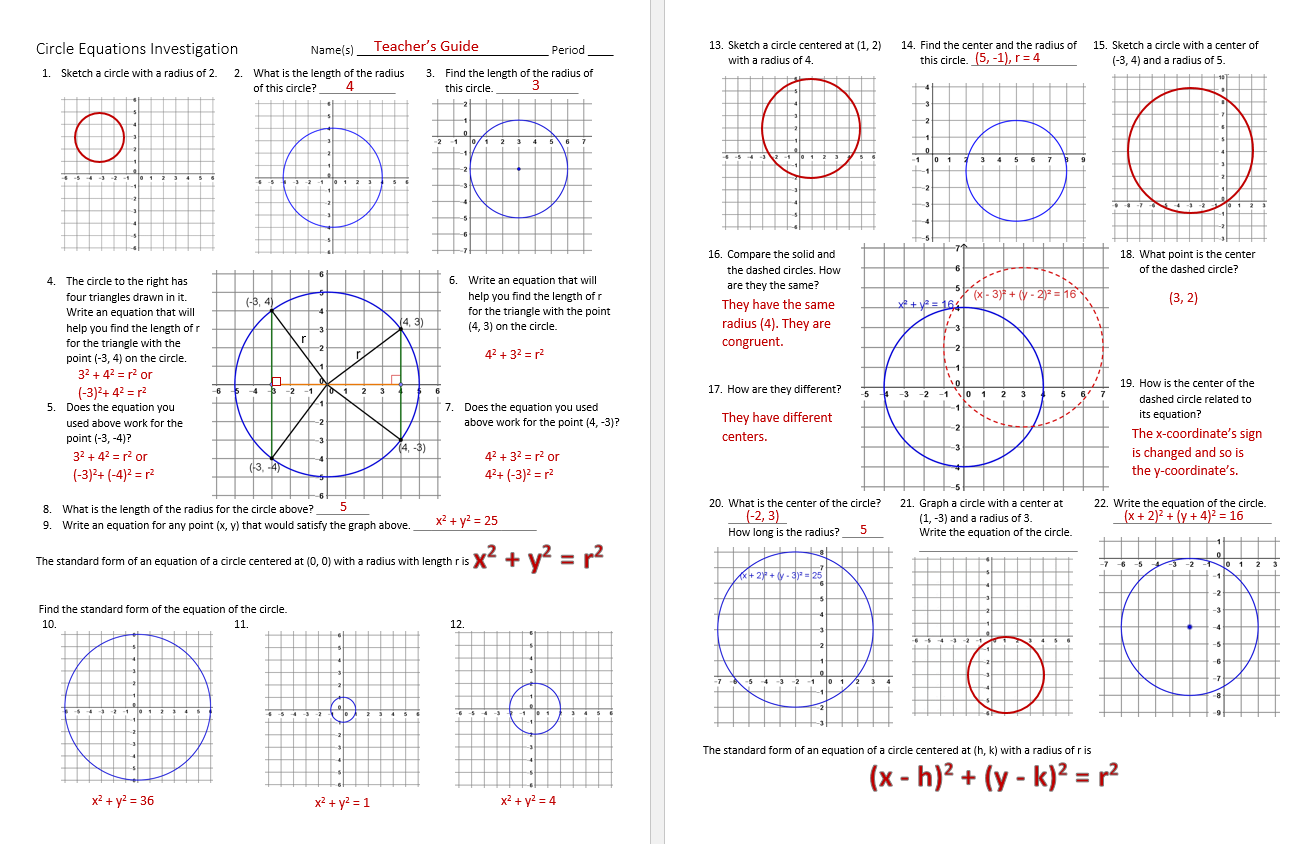
This investigation parallels the Desmos activity. Desmos shines in the second part of the investigation when students can use sliders to change h and k to translate one circle to another’s location. However, where the pencil/paper version excels is the small wins that engage students from the start.
I introduced the topic by stating that I know some of them dislike taking notes to a chorus of a few who stated “I like taking notes”. (The introduction of Vizual Notes in my classes has spawned some “born again math students” who say that Vizual Notes calm them, help them focus, and make learning fun.) Never the less, I told them I wanted to change things up a bit and asked them to start an investigation for me. My plan was to have them work in pairs or groups of three, but my first class was antsy and my instinct said I would lose them quickly if I didn’t guide them as a whole group.
The first question asks them to draw a circle with a radius of 2. I quickly moved up and down the rows prodding students to put their phones away, get out a pencil, etc. as I scanned papers. I commented that every single student except one had drawn the same circle and showed them a circle centered at the origin with a radius of 2. I then showed them what the “non-conforming” student had drawn – a circle centered at some point other than (0, 0) with a radius of 2. Of course that made that one student in each class (and I kid you not, there was exactly one student from each group of approximately 24 that chose a center other than the origin) feel superior.
I asked them to write the answer to question 2 and commended them for not spoiling the surprise by shouting it out. We were on a roll so I asked them to move on to question 3 and write its answer down. Now we had some momentum so I had them to look at question 4 and asked them what I was wanting them to do. One student stated “those are right triangles so we can use the Pythagorean Theorem.” Another raised her hand and asked “Why should we write an equation when we can see the radius is 5?” We launched into a discussion about the usefulness of an equation when there’s an absence of a graph. So they humored me and broke out the Pythagorean Theorem. Some used the coordinates as written, squaring the negative numbers to get positive ones. Others argued that lengths in geometry are always positive so the signs didn’t matter. Then I went to the SmartBoard and plotted a point at an inconvenient location on the circle and asked if that point (2.something, 4.something) would also work with the Pythagorean Theorem. Yes was the answer if the decimals were accurate enough. So I asked them if the point was (x, y), what would the equation be? Wait time… a² + b² = 25. I mean x² + y² = 25. And if the radius is no longer 5 but r instead? And we had our equation of a circle centered at the origin.
“But what if the center is somewhere else?” came a call from a student who sometimes does his work but is often disengaged. “Ah, hold that thought and see if you can answer questions 10, 11, and 12 for me.” And I pop around the room ensuring that some of my struggling students haven’t been left behind in the flurry of new ideas. “Back to your question, please turn over your paper.” And we were on to circles centered elsewhere and developing that equation.
Because I wasn’t sure how long this investigation would take, I gave them a 9 question assignment on this topic with 6 review question. When they came back today, the only question they asked about was one that had an r² that wasn’t a perfect square. As they reviewed for their test, they took those first 3 questions from the image above in stride and said “I need help on question 31; I forgot the distance formula.” I wrote the distance formula on the board and the equation of a circle centered at (h, k) below it asked if they looked similar.
Here is why I think this worked well:
- I was freed from the SmartBoard so I could get students on task and they couldn’t just pretend to be paying attention.
- There were lots of small wins – draw a circle, find the radius – with the chance to point out that my circles don’t look so great either, but we keep trying.
- There was a peppy pace. No chance to be bored.
- My students had to think – not just copy what I was doing.
- They had the necessary skills. We had just come out of a trig unit so the Pythagorean Theorem was fresh in their minds.
- They could all immediately get started – not the case with discharged devices, bad logins, etc. and didn’t have a chance to be distracted by technology.
I have high hopes they do well on four similar questions on their test.
Perhaps next year I will try the Desmos activity with one or more classes and the pencil/paper investigation with a control group and see which is more effective.


Leave A Comment