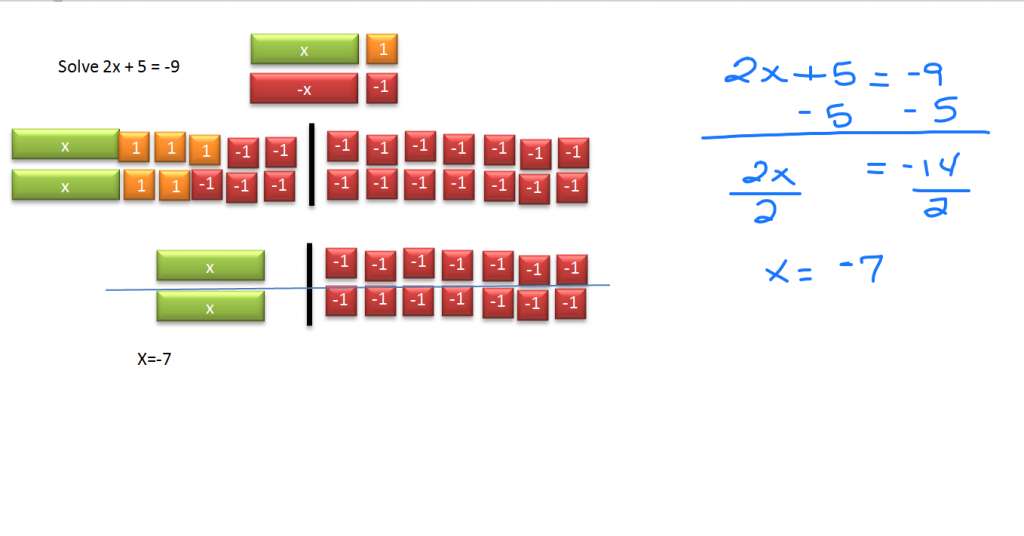
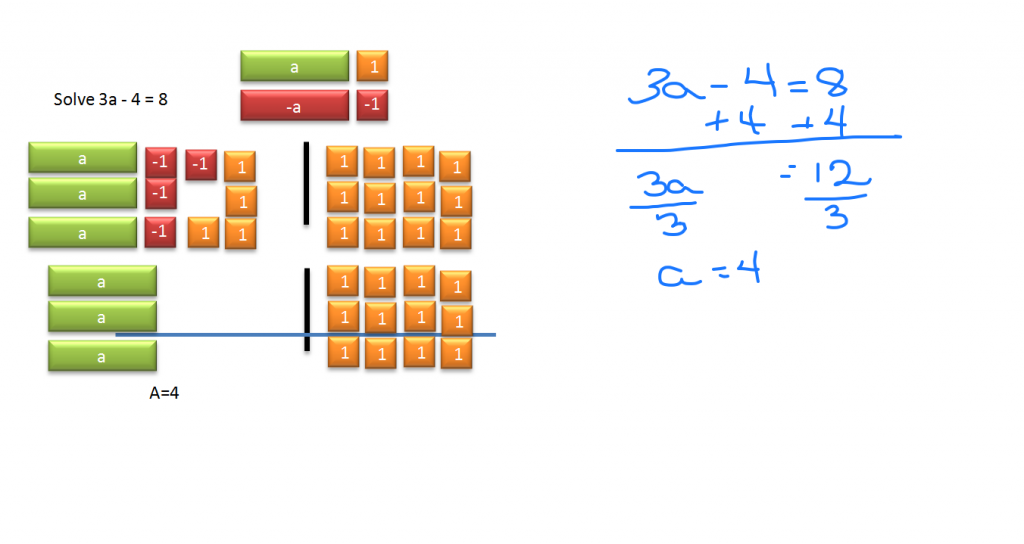
Two step equations require more than one operation to solve. The video above shows how to solve them both visually with Algebra tiles and Algebraically.
Tip: Be sure the tile itself and not the text is selected when making a copy. You can:
- Right click and copy, then paste it where you want it
- Select the tile and press Ctrl + D
- Use the Ctrl + C, Ctrl + V copy and paste short cuts or
- Hold the Ctrl key down while dragging a tile which also makes a copy of the original
Start by isolating the variable (2x). 5 is added to it, so add five -1 tiles to the left to create zero pairs. Balance the equation by adding five -1 tiles to the right side as well.
Simplify by bringing a copy of your two x tiles down. Also copy the fourteen -1 tiles down.
The second step of this solution is to split the tiles evenly. Since two of the x tiles equals fourteen -1 tiles, each single x tile must equal seven of the -1 tiles so x = -7.
Algebraically, if 5 is added to 2x, subtract 5 from both sides of the equation. You are left with 2x = -14. Since two is being multiplied by x, the inverse operation is dividing by two. When you divide both sides by 2, your result is x = -7.
The same process holds here. First get the 3a by itself by adding 4 to both sides. Then because 3a = 12, divide both sides by 3 and a = 4.
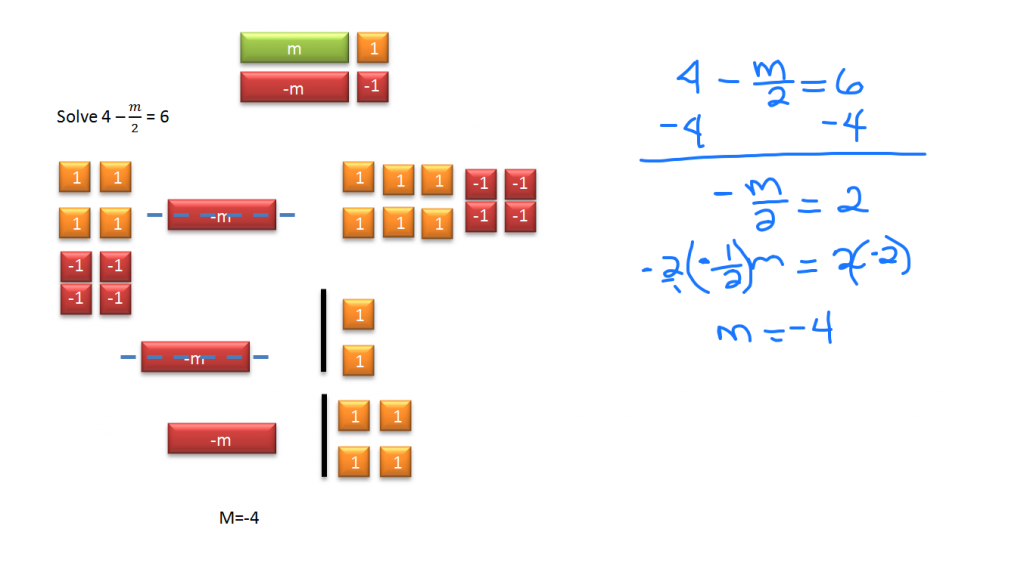 To isolate the m/2, first subtract four from each side. Because m is being divided by two, it must be doubled to get a single full m. So, multiply both sides by 2 (or -2 if you prefer to save a step). The end result is that m = 4.
To isolate the m/2, first subtract four from each side. Because m is being divided by two, it must be doubled to get a single full m. So, multiply both sides by 2 (or -2 if you prefer to save a step). The end result is that m = 4.
Text: Holt, Rinehart and Winston Algebra 1 p 129-134
Next – Multi-Step Equations