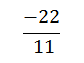Stacie Bender 9/2/14
Just as the order in which you get dressed each morning is important, so, too is the order in which you perform mathematical calculations. By now, you likely have been exposed to PEMDAS often recalled by the phrase “Please excuse my dear Aunt Sally”. It is a reminder to first perform the operations in Parenthesis or grouping symbols. Next, simplify Exponents. Then perform any Multiplication and Division you encounter from left to right. Finally perform any Addition and Subtraction you encounter from left to right. Here’s a hint. If you are working through a problem and are getting very large or complicated numbers, you probably need to start over. Most of the order of operation problems you will encounter can be simplified using mental math.
Example 1
Simplify 2(7 – 3) + 14
According to PEMDAS, the parenthesis or grouping symbols must be simplified first. Don’t be afraid to use some pencil lead. Writing out your steps is a kinesthetic activity that helps you learn and remember. Since 7 – 3 = 4, re-write the expression with the 4 in the parenthesis.
2(4) + 14
Everything in the grouping symbol is simplified so next we check for Exponents. There are none, so we then look for Multiplication and Division from left to right. 2(4) is a multiplication problem. We get
8 + 14
22 is our final result.
Example 2
30 ÷ 5 • 2
Using PEMDAS, we note there are no Parenthesis nor Exponents. The next step is to look for Multiplication and Division from left to right. So, reading from left to right, what do we encounter first?
30 ÷ 5 Don’t fall for the “I’ll multiply first because PEMDAS lists M before D” trap. The result is
6 • 2
12
Note that if you do not follow the order properly you would have multiplied first to get 30 ÷ 10 or 3. There’s a big difference between the two.
Example 3
7 +
In this example, note there are two sets of grouping symbols. Start with the inner most and work your way out.
(3 + 3²) can’t be cleared until the exponent is simplified. When we square 3 we get 9 so we now have
7 + [24 ÷ (3 + 9)]
Now clear the inner parenthesis.
7 + [24 ÷ (12)]
The parenthesis around the 12 is not absolutely necessary. Next clear the outer grouping symbols – the brackets by performing the division.
7 + [2]
9
A good scientific or graphing calculator can help you check yourself, but if you don’t enter the equation properly, it can give the wrong answer. Always rely on your brain to perform the work and use the calculator to verify your work. Do not let the calculator become a crutch.
Example 4
Simplify
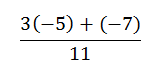
Think of the division bar as one big grouping symbol. Evaluate the numerator (top) first. Multiplication is first.
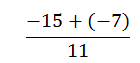
Remember + (- 7) is the same as – 7.
Since 15 and 7 are both negative, add them and give them the negative sign.
-2