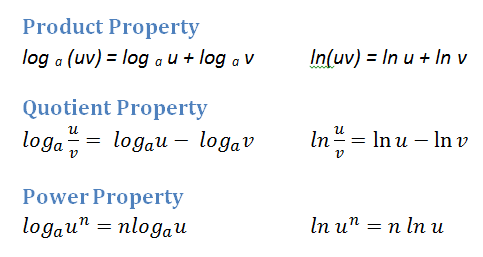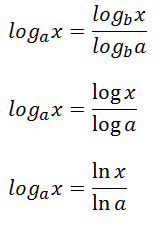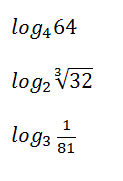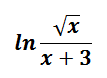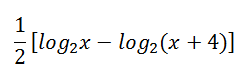As you have probably noticed, your calculator only has two log buttons: the common log, log 10 and the natural log, log e or ln. Fortunately, by using the change of base theorem, you can evaluate a log of any base.
Change of Base Theorem
Evaluate
Round the result to three decimal places.
log 6 9
Take the log of 9 divided by the log of 6. The result is 1.226.
log 2 14
Divide the log of 14 by the log of 2 The answer is 3.807.
log 1/4 12
You can also use the natural log instead of the common log. Take ln 12 / ln .25. The result is -1.792.
Evaluate
Do not use a calculator.
Properties of Logarithms
Because the answer to a logarithmic equation is the exponent in an exponential equation, it makes sense that logarithms should behave as exponents do.
Expand
log 5 3x2y
Condense
3 ln(x – 5) + ln x
Precalculus with Limits – Larson & Hostetler p.239-245