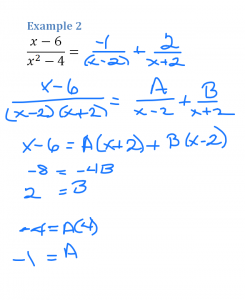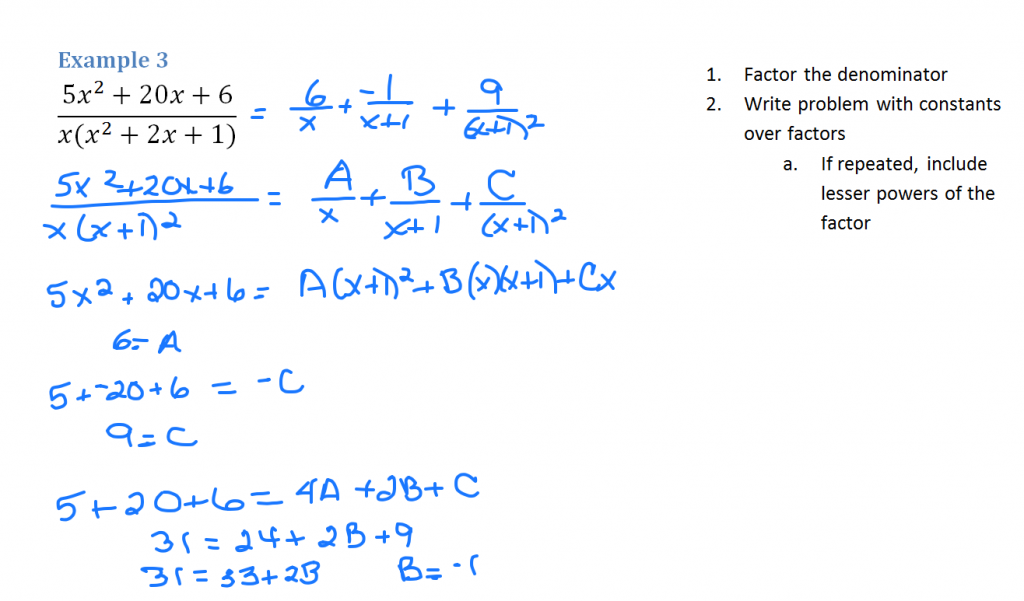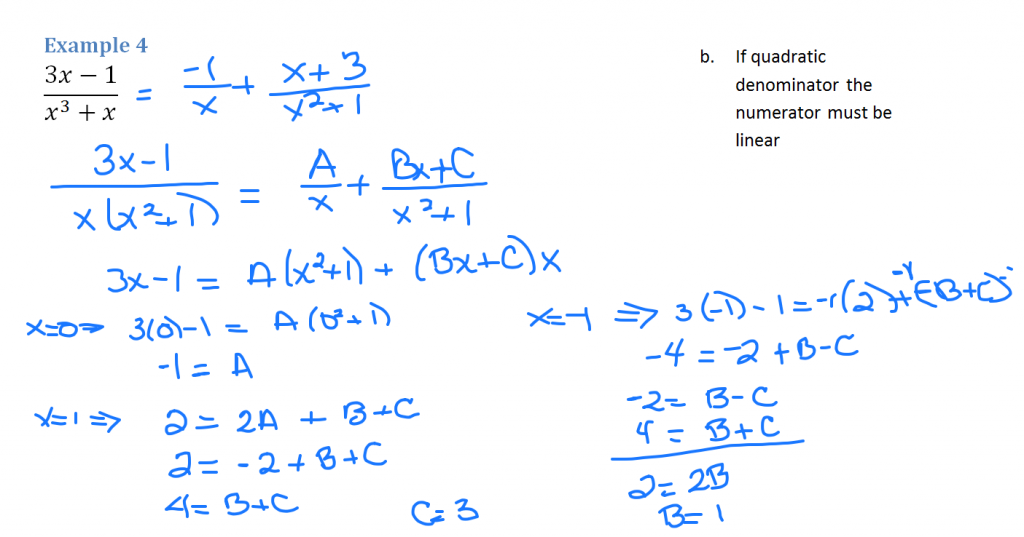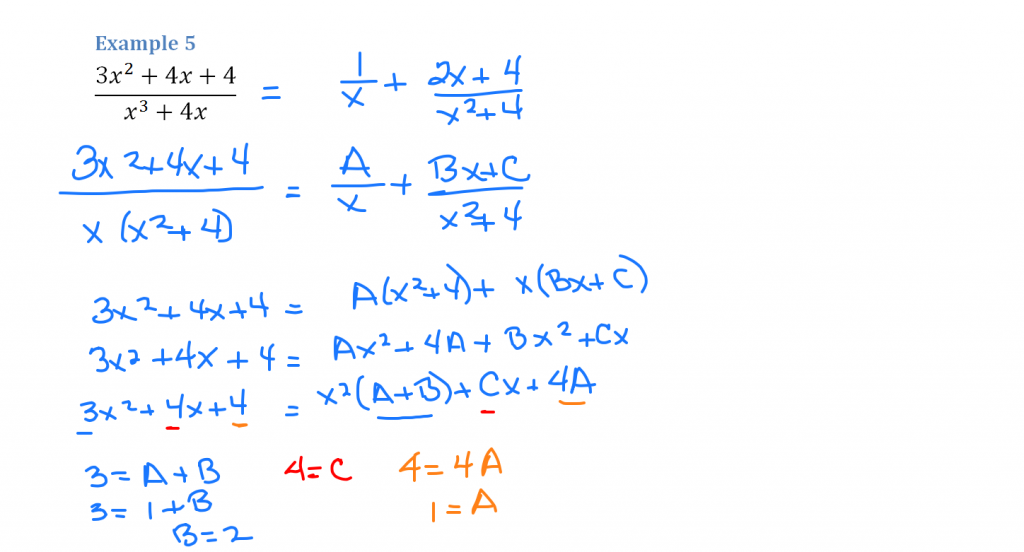Start by rewriting the fraction with its factored denominator. Set it equal to some number A over its first factor plus a number B over its second factor. Simplify by multiplying each term by the LCM. The left side becomes x + 7. On the right you will have A(x + 2) plus B(x – 3).
To simplify, substitute numbers for x that will make zeros in the equation. If x is -2, A disappears and you are left with 5 = B(-5) so B = -1. To eliminate B from the equation, let x be 3. Subbing in 3 for x leaves 10 = 5A so A = 2. Now re-write the partial fraction.
Skip to 04:02 in video for example 2
Factor the denominator. Write as partial fractions with constants A and B. Multiply each term by the LCM. Then pick convenient values for x that eliminate each constant in turn. When x = -2, the A is eliminated. When x = 2, the B is eliminated. Re-write with the constants in place.
Skip to 06:34 for example 3
Follow the same process, but because the denominator factors into (x+1) squared, it has to be repeated with both the squared factor and its lesser factor. We introduce a C constant to our third fraction.
Eliminate the easy ones by substituting 0 for x and also -1 for x. To determine the value of B, substitute 1 for x (along with the values for A and C).
Skip to 11:26 for example 4
Example 4 requires a numerator that’s linear because one of the factors of the denominator is a quadratic. Start by writing A over x then Bx + C over the quadratic factor of x² + 1. Multiply by the LCM to clear the fractions. Substitute 0 and 1 for x to simplify. Then pick another value for x to get another equation with two of the constants. Use a system of two equations with two unknowns to solve.
Skip to 17:19 for example 5
The trick to example 5 is to notice that you have a quadratic on the left side once the denominators are eliminated. That means the coefficients of x² are equal, the coefficients of x are equal and the constants are equal.