Just as addition is the inverse of subtraction and multiplication and division are inverses of one another, logarithms and exponents are inverse operations.
Definition of a Logarithmic Function with Base a
A logarithmic function is defined as y = loga x if and only if ay = x
For x > 0 and a > 0, and a ≠1
That means the answer to a logarithmic equation is the exponent of an exponential equation.
How would we write the following in exponential form?
Log10 100 = 2
Log3 81 = 4
Write the following in logarithmic form.
28= 256
53 = 125
170 = 1
Properties of Logarithms
loga 1 = ________ because
loga a = ________ because
log a ax = ________ because
If log a x = log a y then
Solve the following:
log 4 16 =
log 6 1 =
log 9 3 =
log 2 (-1) =
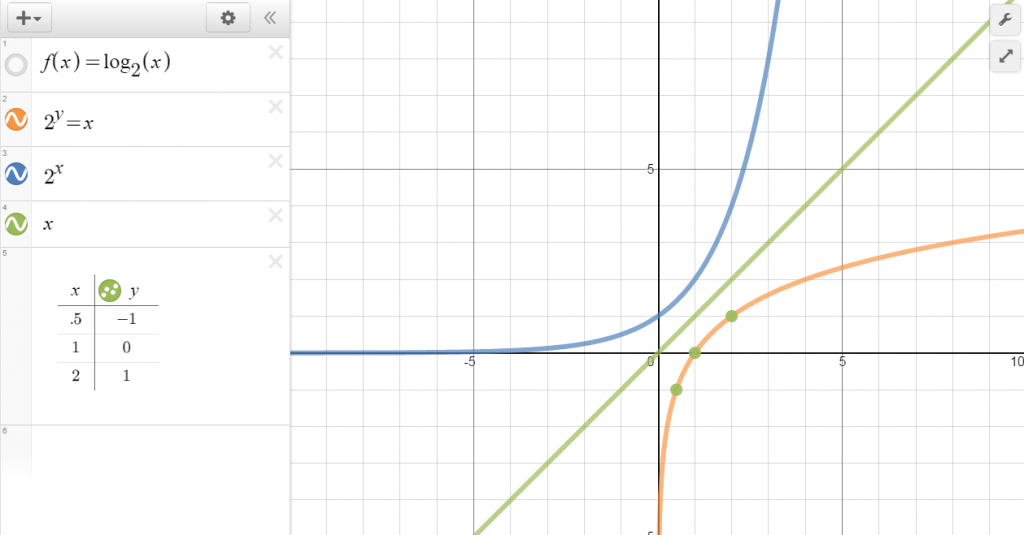
Graph y = log 2 x
Start by writing it in exponential form.
2y = x
Now, plug in values for y.
This should remind you of a function you have been introduced to earlier:
f(x) = 2x
How are the two related?
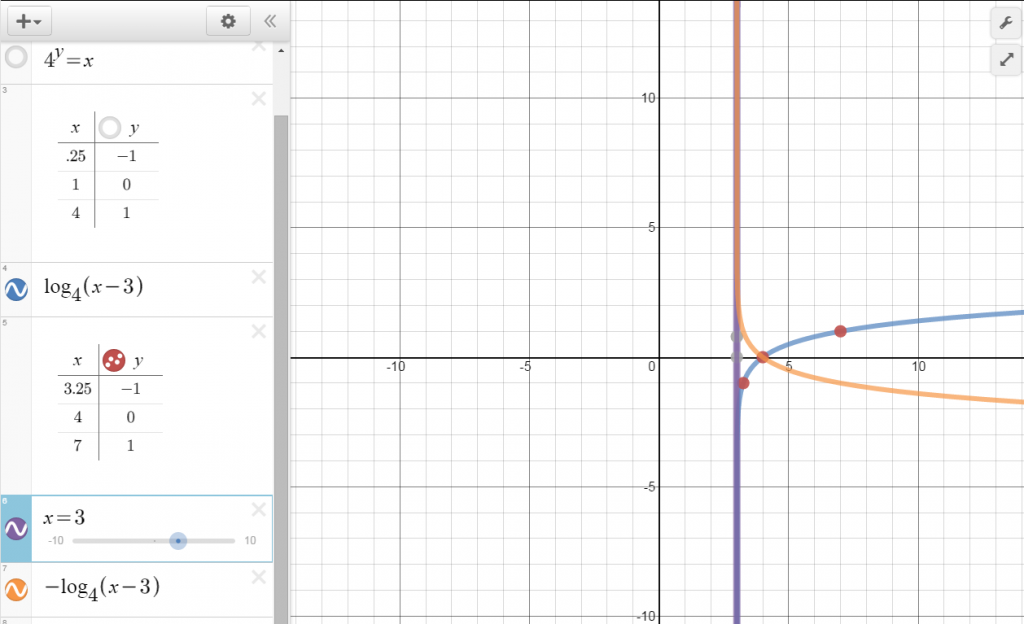
Graph y = log 4 (x – 3)
Remember your families of graphs? Start by graphing your parent function of y = log 4 x. Then shift it 3 to the right.
The Natural Log
e – Euler’s Number, Napier’s Constant, the Natural Base
e ≈ 2.718281
e is the base in the natural log noted as ln.
So ln = loge ≈ log 2.718
Graph y = ln x
Graph y = -ln (x – 1)
Because order of operations says to do what’s in parenthesis first, shift left one first, then reflect across the x-axis.
If your logarithmic function involves a reflection and a vertical shift like this function – y = -ln x + 2, first reflect over the x – axis, then shift up 2 because the multiplication of the -1 would take place before the addition of 2.
Solve log 12 (x – 3) = log 12 (2x + 5)
Precalculus with Limits – Larson & Hostetler p. 229-238