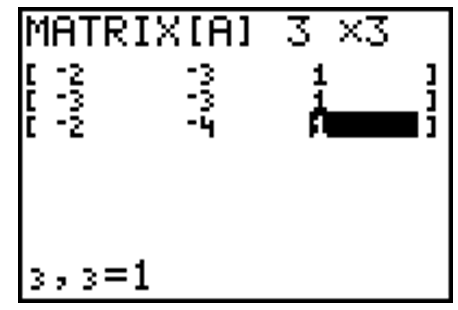
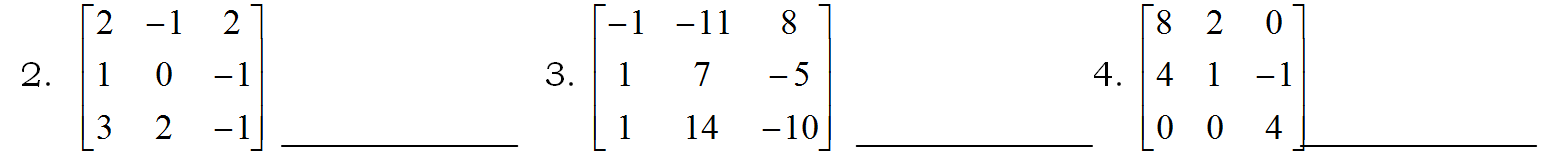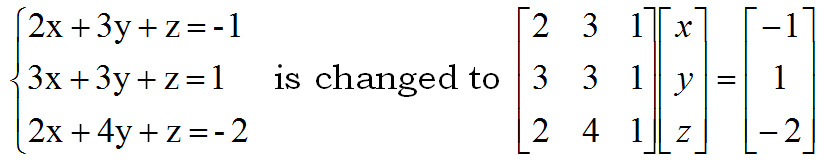One method of finding the inverse of a 3×3 matrix involves using a graphing calculator. Store the following matrix into
[A].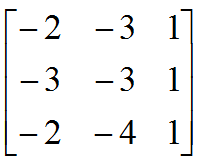
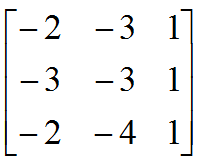
- Press the 2nd key, then MATRIX (2nd of x-1)
- Arrow to the right to the EDIT menu, then press ENTER to edit matrix [A]
- Type a 3, arrow to the right and type a 3 to tell your calculator it’s a 3×3 matrix.
- Press ENTER and begin typing the entries above into the matrix, using the ENTER key to advance to the next entry. When you are finished you calculator should look like this.
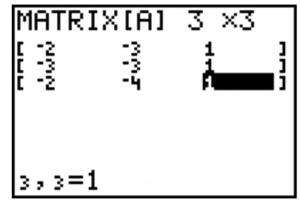
- Press 2nd then QUIT. Press the MATRIX button again, press ENTER to place [A] on the home screen, then press the x-1 button to ask for the inverse of matrix A. Press ENTER to display A-1 and write the answer below.
___________________
Find the inverses of the following matrices.
Matrices can be used to solve systems of equations. The following equations are changed to matrices, the inverse of the first matrix is multiplied by the last matrix and the result is the solution to the system.
The system
Store the first matrix in [A], the second (the “answer” matrix) in [B]. Then take [A]-1 times [B].
- Write your result. x = _________, y = __________, z = __________
- Find the solution to the system
3x + 2y – z = 11
2x – y + 2z = -3
x + 3y – z = 8
x = _________, y = __________, z = __________
A printable version of this page is available for classroom use. Finding Inverses of Matrices