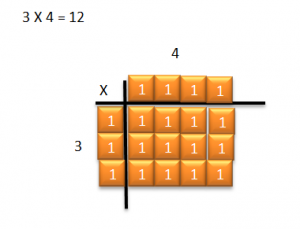Stacie Bender 8/20/14
Algebra tiles have been available for years.
Positives:
- They can make the abstract more concrete.
- They help both visual and kinesthetic learners understand the concepts of Algebra.
Negatives:
- It can be costly to acquire enough tiles for classrooms to share.
- They require maintenance in getting the tiles back into the bags in the right numbers.
Electronic Algebra tiles can be a solution to these issues provided students have access to a word processing program.
The following video demonstrates how to use Algebra tiles to multiply binomials.
In elementary school you probably used blocks, tiles or grids to demonstrate multiplication. The process may have went like this:
What is 3 x 4?
You would select three tiles and place them down one dimension of your multiplication table, place four tiles along the other dimension, fill in the rectangle created by the tiles and then count the result.
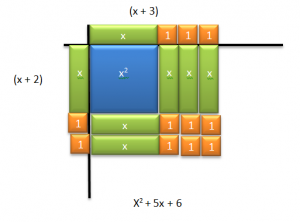
You can use the same idea when multiplying Algebraic expressions. For example, if we want to know the product of x + 2 and x + 3, we can use Algebra tiles to find the answer.
Notice the different types of tiles here. X squared is a square that’s x by x in size. The green tiles are rectangles that are 1 by x in size. The red rectangles are negative 1 by x in size and the orange and red squares are positive 1 and negative 1 in size.
To find the product of x + 2 and x + 3, place an x and two ones along the left side of your multiplication table. In Word you can duplicate shapes by selecting them and pressing Ctrl +the letter D. Be sure you see the move icon signaled by four arrows when dragging them to the table. Then place an x and three ones along the top of your table. Next, fill in the area inside your table to create a rectangle. X times x is x² . X times 3 is 3 x’s. Two times x is 2x and 2 times 3 is 6. Finally, read the resulting area. x² + 5x + 6.
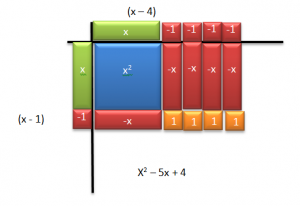
Let’s try a problem with negative values. Multiply (x – 1)(x – 4). Again we choose the green x tiles, but this time we need red ones tiles. When we fill in the area below the multiplication table, we must ask ourselves what is a positive x times a positive x? Positive x². What is a positive x times negative four? Negative four x’s. What’s positive x times negative 1? Negative x. Finally, what’s negative 1 times negative 4? Positive 4. Fill in the area, then write the result. x² – 5x + 4
Teacher Demonstration File – Multiply Binomials Teacher Demo
Student Practice File – Multiplying Binomials Student Activity
Holt, Reinhart, Winston Algebra I p. 432 – 442
Additional Resource – Using Algebra Tiles Effectively