Stacie Bender 9/15/14
An exponential function is a function in which the variable is an exponent. What would that look like? When we say something is a function, we begin with function notation:
f(x) =
Since the variable must be the exponent, we need a constant or a number to the power of x.
f(x) = ax
So f(x) = 7 x, f(x) = ½ x, and f(x) = .4x are all exponential functions.
Is f(x) = x 2 an exponential function? No, the exponent has to be the variable.
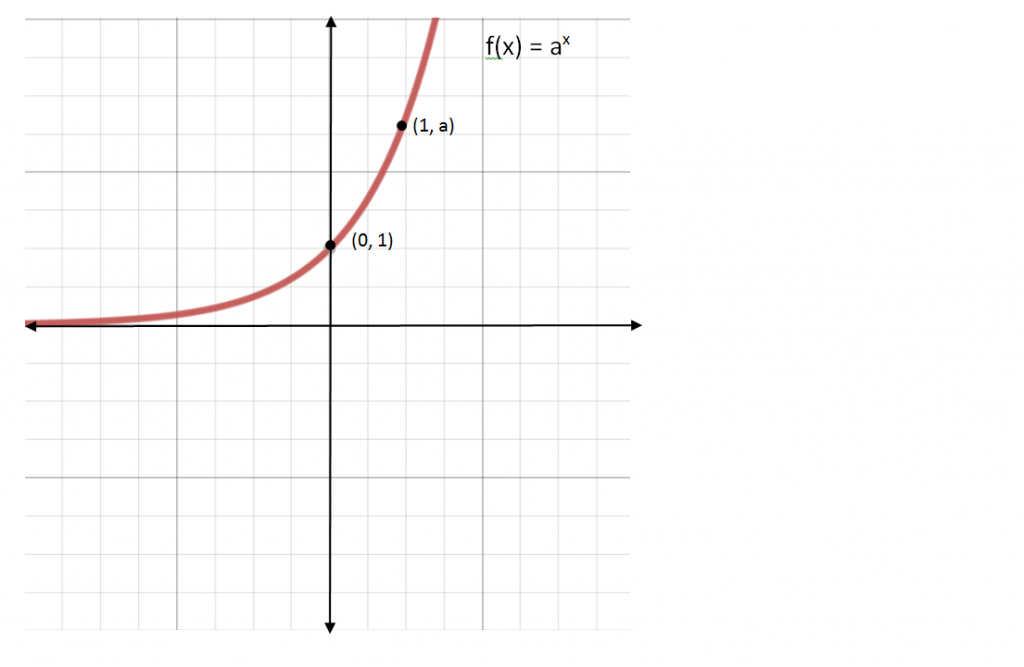
Exponential functions are defined where a > 0 and x is any number.
Looking at this graph of f(x) = ax, what is the domain?
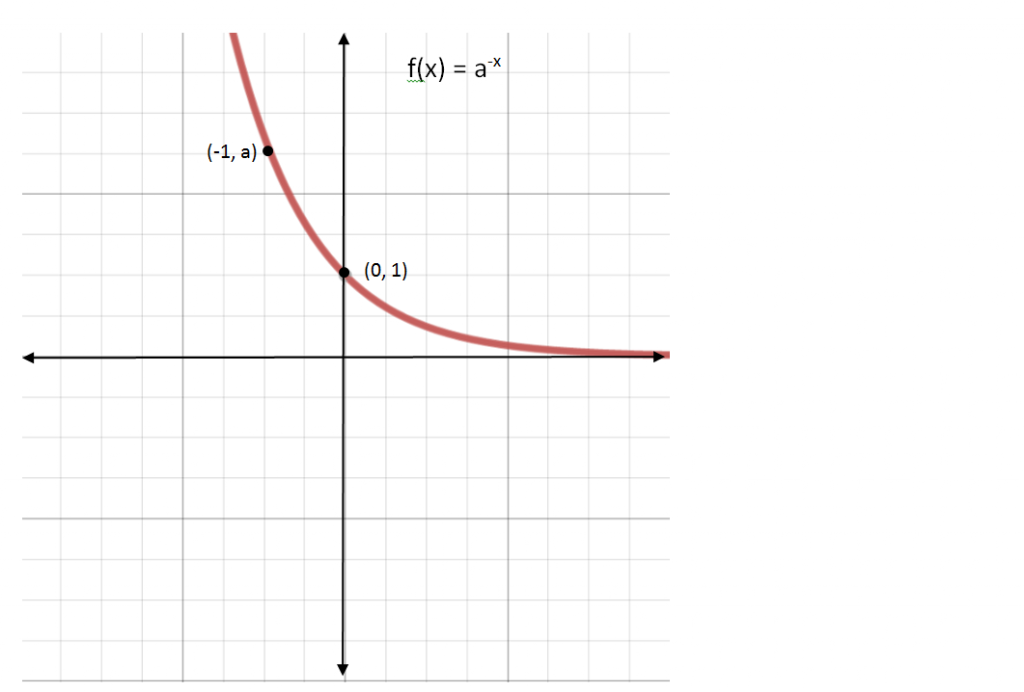
Looking at the graph of f(x) = a-x, what is the domain?
What is the range?
Where is it increasing?
Decreasing?
What is the y-intercept?
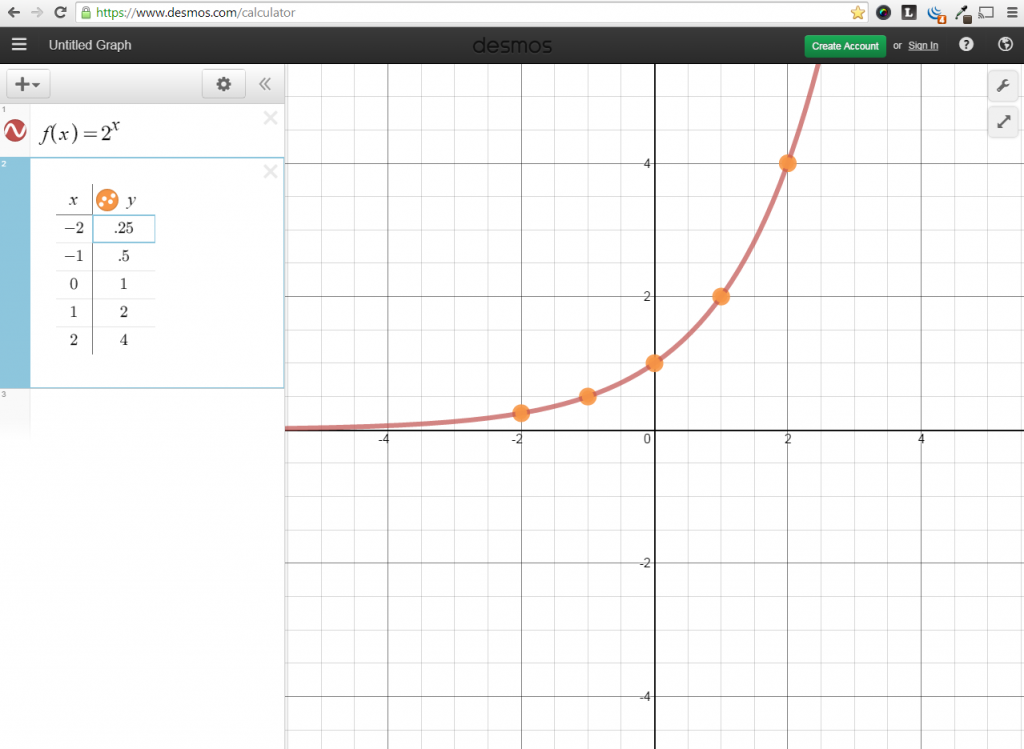
Graph an Exponential Function
Graph f(x) = 2x
Families of Graphs
f(x) = a (x – h) + k
a – stretch (amplitude)
h – horizontal movement
k – vertikal movement
If f(x) = 2x, describe the transformation when g(x) = 2x + 3
Describe the transformation when h(x) = 2-x – 4.
e – Euler’s Number, Napier’s Constant, the Natural Base
e is an irrational number that’s important in Calculus limits, continuously compounded interest, and exponential decay. It is an irrational number.
e ≈ 2.718281
e is the base in the natural log noted as ln.
So ln = loge ≈ log 2.718
Compound n times/year Continuously Compound
A =
P =
n =
r =
t =
If you loaned a bank $10,000 at a 5% interest rate for 10 years, find out the amount you would have in the bank if it is compounded:
Monthly
Continuously
Precalculus with Limits – Larson & Hostetler p 218 – 228